I have colour-coded all 4 program listings as a learning aid to readers new to programming. I encourage beginners to try colour-coding whatever program listings they encounter; this will provide a leg up on programming.
- Built-in commands intrinsic of the programming language appear in blue. These we can't change as we like, or we knock the program out of order.
- Variables defined by the user appear in red. These we can change according to our liking. Take Listing 1, for example, we can replace all occurrences of out to donkey, alice or smile, and the program will still sing and dance all the same. The worse we could do would be to confuse ourselves, wondering what is the donkey's role here or what is Alice doing here. So, best to name variables meaningfully — when you revisit the program next time, or if you pass the program to someone else, your program will be less painful to decrypt.
- Instantaneous values appear in limegreen. In computing terms, values may be numbers or characters.
out = fopen('dominance.mout','w');
file = dir('*.txt');
for f = 1:numel(file)
lastflag = 0;
field = strsplit(file(f).name,'.');
Z = str2num(field{1});
fprintf(out,'%d ',Z);
a = importdata(file(f).name,' ',3);
for row = 1:size(a.data,1)
E = a.data(row,1);
compt = a.data(row,3);
photo = a.data(row,4);
pairp = a.data(row,5) + a.data(row,6);
if (photo>compt && photo>pairp)
thisflag = 1;
elseif (compt>photo && compt>pairp)
thisflag = 2;
elseif (pairp>photo && pairp>compt)
thisflag = 3;
end
if (lastflag==1 && thisflag==2)
fprintf(out,'%.3e ', E);
elseif (lastflag==2 && thisflag==3)
fprintf(out,'%.3e\n', E);
elseif (thisflag~=lastflag && lastflag>0)
fprintf(out,'Exception! %.3e %d\n', E, Z);
end
lastflag = thisflag;
end
end
fclose(out);
b = load('dominance.mout');
hold on
plot(b(:,2),b(:,1),'r.')
plot(b(:,3),b(:,1),'bx')
set(gca,'xscale','log')
legend('Photoelectric to Compton','Compton to Pair','location','northwest')
legend boxoff
xlabel('Photon energy (MeV)')
ylabel('Atomic number')
grid on
Listing 2. Matlab script for this exercise; works equally well in Octave. ☞ download
import glob
import numpy as np
import matplotlib.pyplot as plt
out = open("dominance.pyout","w")
for file in glob.glob("[0-9]*.txt"):
lastflag = 0
field = file.split(".")
Z = int(field[0])
out.write("%d " % Z)
with open(file) as xcom:
for tisline in xcom.readlines()[3:]:
field = tisline.split()
E = float(field[0])
compt = float(field[2])
photo = float(field[3])
pairp = float(field[4])+float(field[5])
if (photo>compt and photo>pairp) :
thisflag = 1
elif (compt>photo and compt>pairp) :
thisflag = 2
elif (pairp>photo and pairp>compt) :
thisflag = 3
if (lastflag==1 and thisflag==2) :
out.write("%.3e " % E)
elif (lastflag==2 and thisflag==3) :
out.write("%.3e\n" % E)
elif (thisflag!=lastflag and lastflag>0) :
out.write("Exception! %.3e %d\n" % (E,Z))
lastflag = thisflag
out.close()
b = np.loadtxt("dominance.pyout")
plt.plot(b[:,1],b[:,0],'r.')
plt.plot(b[:,2],b[:,0],'bx')
plt.gca().set_xscale('log')
plt.xlabel('photon energy (MeV)')
plt.ylabel('Atomic number')
plt.grid(True)
plt.show()
Listing 3. Python script for this exercise. ☞ download
open(out,">dominance.plout");
while(defined( $file=glob("[0-9]*.txt") )) {
open(xcom,$file);
$lastflag = 0;
@field = split /\./, $file;
$Z = $field[0];
printf out "%d ",$Z;
<xcom>; <xcom>; <xcom>;
while($thisline = <xcom>) {
@field = split /\s+/, $thisline;
$E = $field[0];
$compt = $field[2];
$photo = $field[3];
$pairp = $field[4] + $field[5];
if ($photo>$compt && $photo>$pairp) {
$thisflag = 1;
}
elsif ($compt>$photo && $compt>$pairp) {
$thisflag = 2;
}
elsif ($pairp>$photo && $pairp>$compt){
$thisflag = 3;
}
if ($lastflag==1 && $thisflag==2) {
printf out "%.3e ",$E;
}
elsif ($lastflag==2 && $thisflag==3) {
printf out "%.3e\n",$E;
}
elsif ($thisflag!=$lastflag && $lastflag>0) {
printf "Exception! %.3e %d\n",$E,$Z;
}
$lastflag = $thisflag;
}
}
close(out);
Listing 4. Perl script for this exercise. ☞ download
set logscale x
set xlabel "Photon energy (MeV)"
set ylabel "Atomic number"
set key left top
set grid
plot "dominance.plout" using 2:1 title 'Photoeletric to Compton', \
"dominance.plout" using 3:1 title 'Compton to Pair'
Listing 5. GNUplot script for this exercise. ☞ download
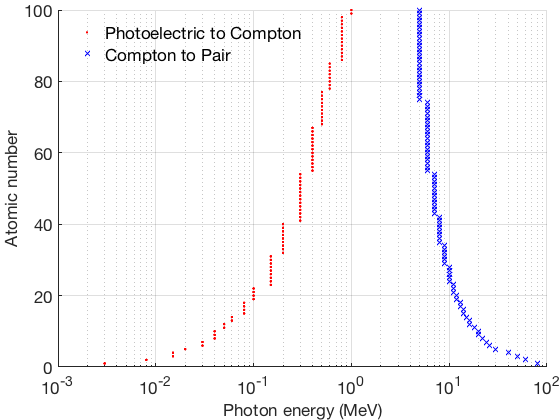
Figure 2. The outcome of this exercise.
Dominance of photon cross sections for Z = 20.
| energy range | dominant interaction |
|---|
| E < 0.1 MeV | photelectric absorption |
| 0.1 MeV < E < 12 MeV | Compton scattering |
| E > 12 MeV | pair production |